PhD position in Mathematics, specialization in Algebraic Geometry & Neural Network Theory

KTH Royal Institute of Technology, Stockholm

Application deadline • May 12, 2025 11:59 PM CET

How to apply• go here and click on apply here on the right-hand side of the page

Contact • Kathlén Kohn kathlen@kth.se

The successful candidate will pursue a PhD project at the intersection of algebraic geometry and neural network theory under the supervision of Kathlén Kohn. The position is a full-time, five-year position starting September 2025 or at an agreed upon date. The student will be enrolled in the Doctoral program in Mathematics. The successful candidate will be part of the Kathlén Kohn's vibrant research group on Algebraic Geometry in Data Science and AI, consisting of 2 postdoctoral researchers and 4 PhD students working on Algebraic Computer Vision or Algebraic Neural Network Theory, and several co-advised PhD students. The group collobarates closely with several computer vision and machine learning groups in Sweden and internationally, and is one of the many diverse research groups in algebraic geometry in Stockholm. Students interested in fields related to the following are encouraged to apply: algebra, geometry, machine learning theory, data science.

Project proposal: Algebraic Neural Network Theory

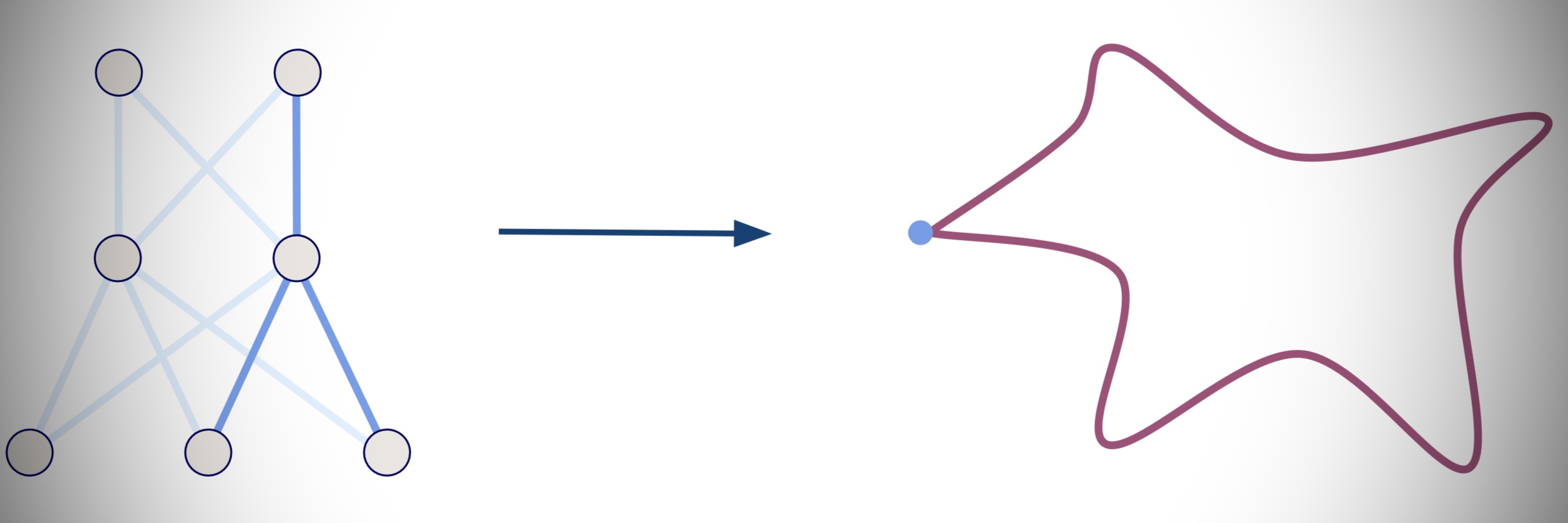
We will study neural networks with polynomial (or more generally, piecewise rational) activation functions. The benefits of this setting are: 1) Such networks can be investigated with algebraic geometry and 2) they can approximate arbitary networks. We will be particularly interested in understanding the set of functions parametrized by a fixed network architecture when varying the weights. This set is a (semi)-algebraic variety in out setting, called neurovariety. For example, the blue set is the neurovariety of (small) self-attention mechanisms, the key ingredient in transformers in large language models such as ChatGPT.
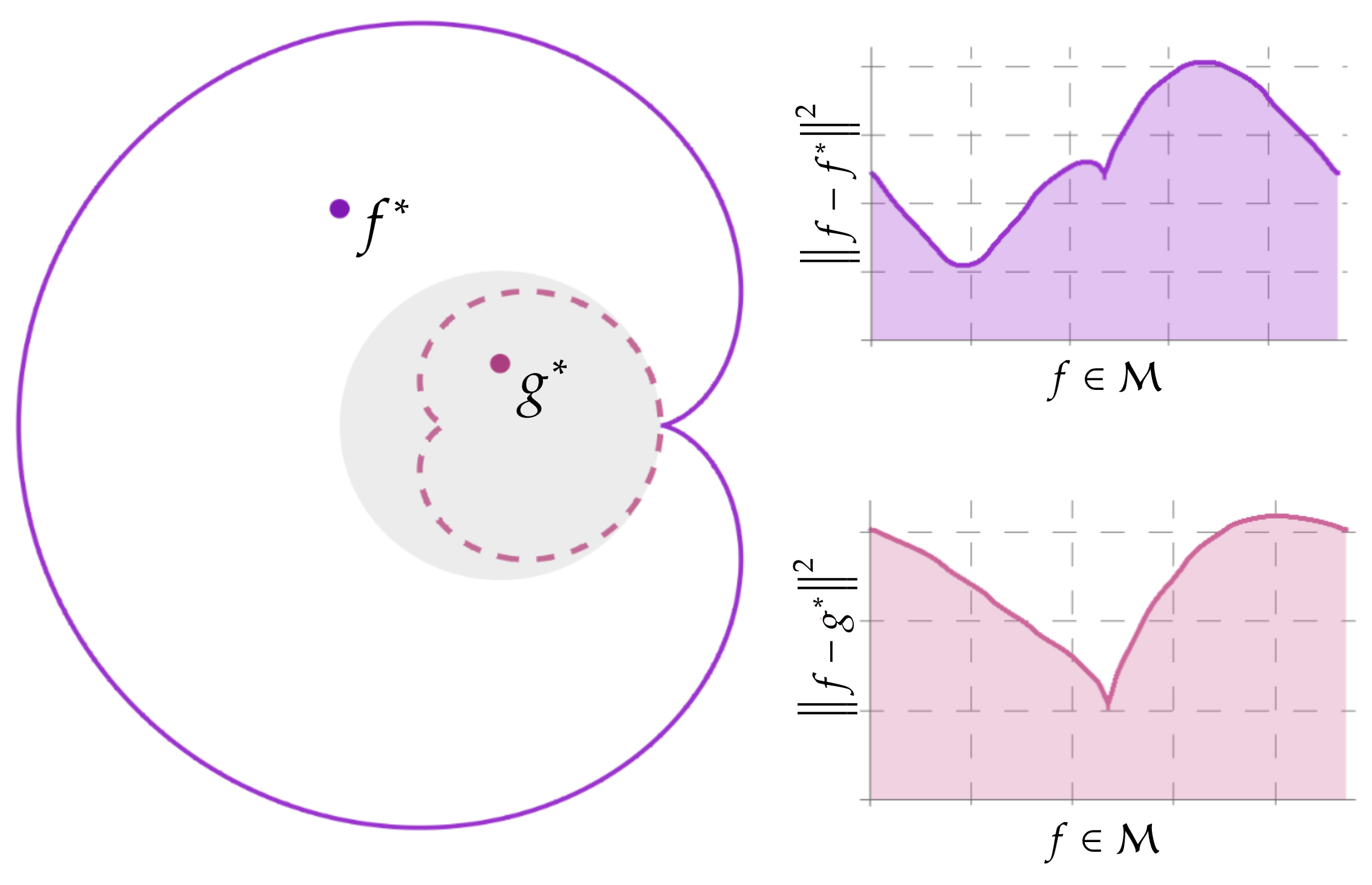
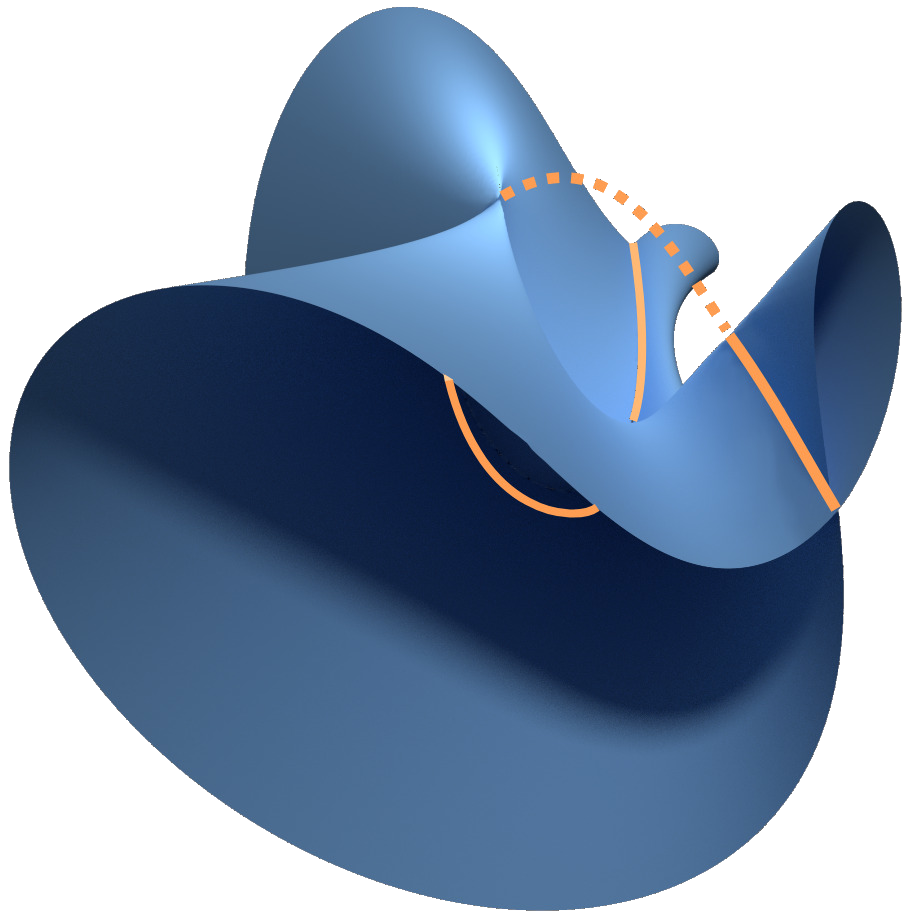
Network training can be interpreted as finding the "closest" point on the neurovariety from the training data (as in the figure with the yellow variety). We will study the properties of this optimization problem. For instance, we will investigate the loss landscape via algebraic discriminants (see figure on bottom left) and the effect of singularities on implicit bias towards subnetworks (see figure on bottom right). For an introductory reading into this growing area, see our Invitation to Neuralgebraic Geometry.