Postdoctoral position in Algebra-Geometric Foundations of Deep Learning or Computer Vision
KTH Royal Institute of Technology, Stockholm
Contact • Kathlén Kohn kathlen@kth.se
The research group on Applied Algebraic Geometry in Data Science and AI led by Kathlén Kohn at the Department of Mathematics at KTH Stockholm has an open postdoctoral position:
- Starting date: upon agreement, in 2026
- Duration: employment for 2 years, with the possibility of extension by 1 more year
- Requirements: a doctoral degree or an equivalent foreign degree
- How to apply: read the instructions here and click on Apply here on the right
- Application deadline: January 16, 2026
The position is financed by Kathlén Kohn's Swedish Foundations' Starting Grant Algebraic Vision. The overarching goal of the project is to develop the algebra-geometric foundations for 3D scene reconstruction from images taken by unknown rolling-shutter cameras, which is the overwhelming camera technology of today. Due to the important role that deep learning plays in modern reconstruction implementations, Kathlén Kohn's research group is also developing an algebraic theory of deep neural networks to facilitate both the understanding of why deep learning works so well (or which aspects do not) and the design of more efficient neural networks. The successful applicant will work either on 3D reconstruction or deep learning theory (or both), in either case with a strong focus on algebraic and geometric tools and understanding. For more details on the two project aspects, see below.
The successful candidate will be part of the vibrant and diverse research groups in algebraic geometry and data science in Stockholm.
Required profile
Besides a doctoral degree as specified above, the successful candidate is expected to have:
- a strong background in one of the following: algebraic, complex, differential, or discrete geometry, mathematics of deep learning, or mathematics of computer vision,
- written and spoken English proficiency, very good communication and teamwork skills, in particular a willingness to collaborate with both engineers and mathematicians, and
- strong motivation and ability to work independently.
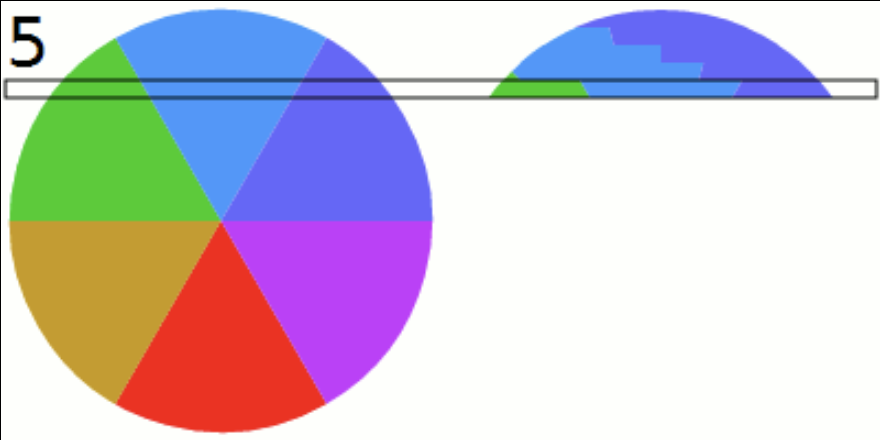
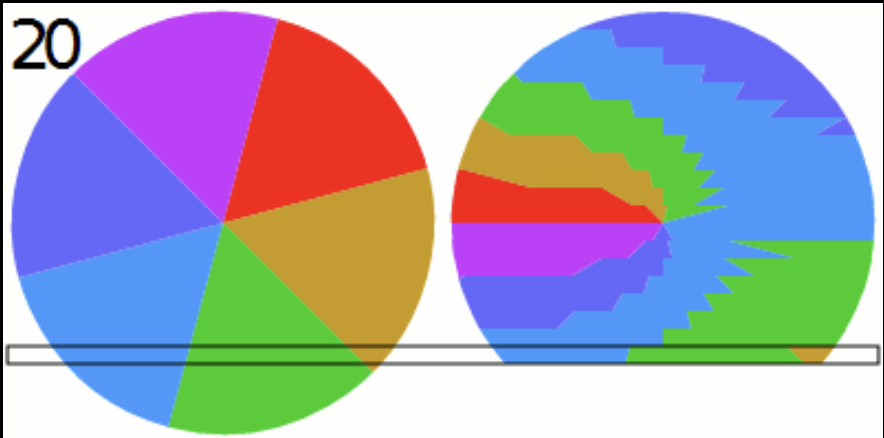
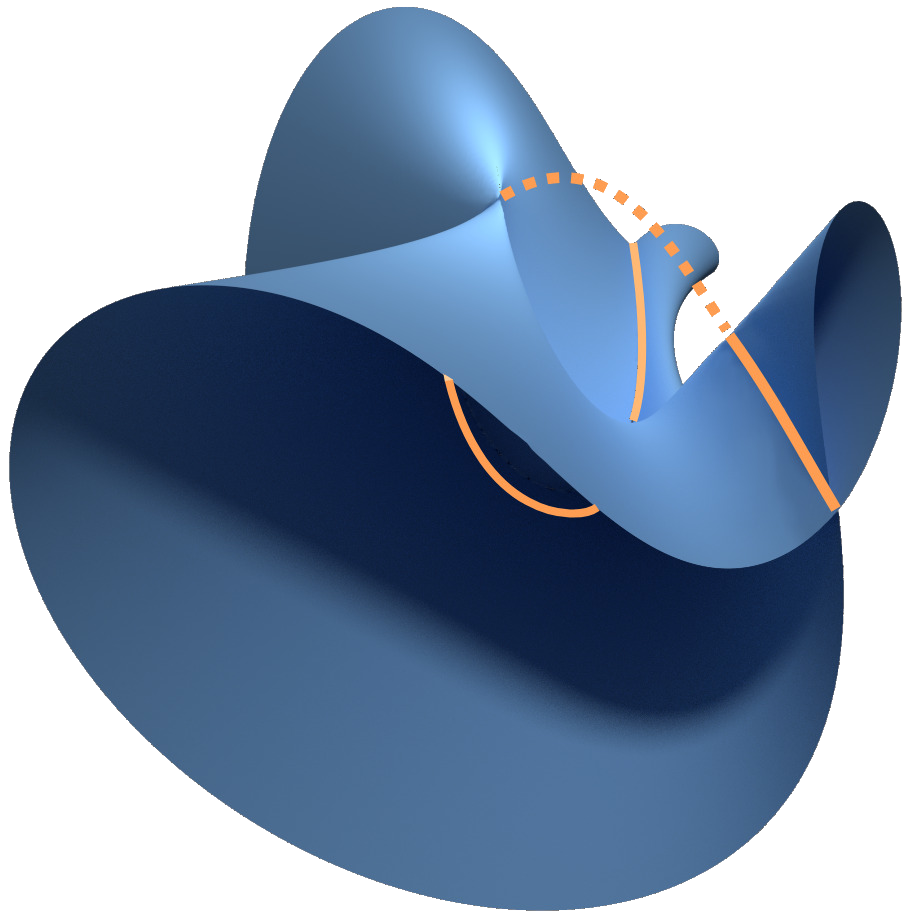Neuromanifold of a self-attention network.
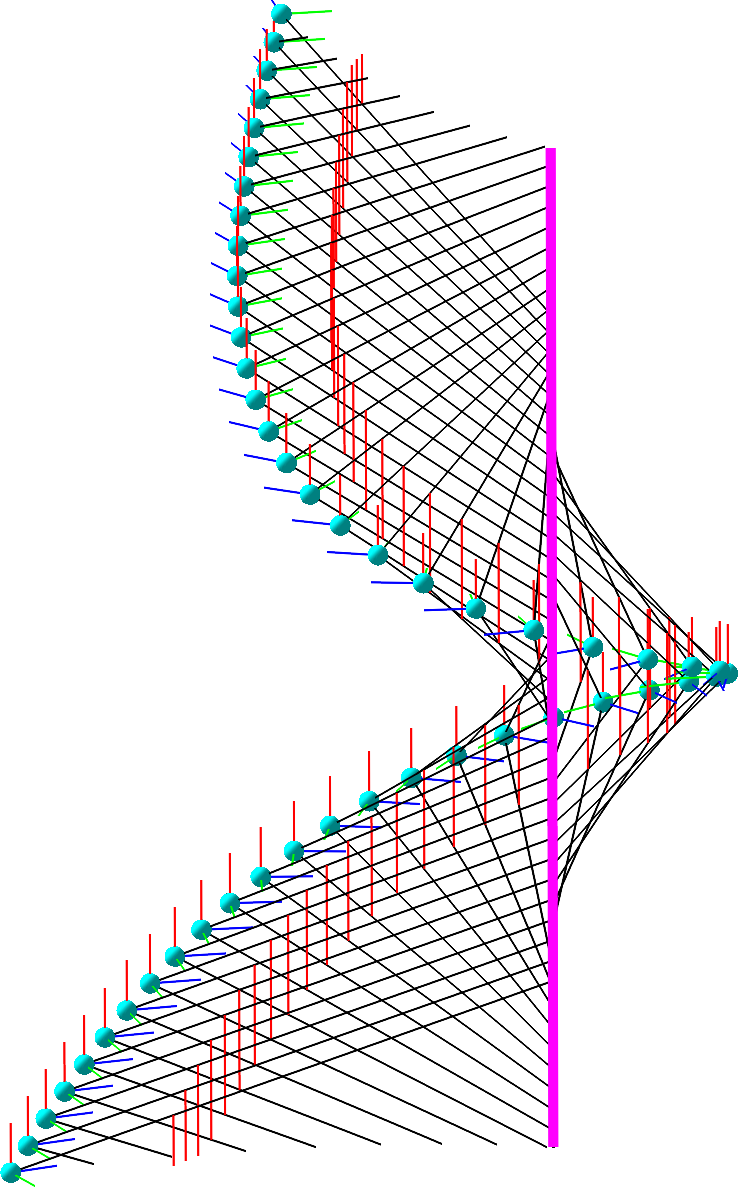
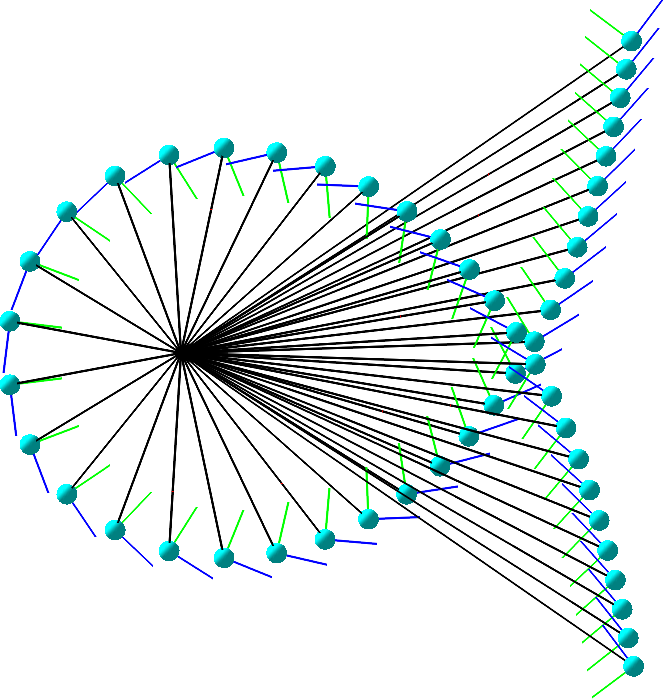
Algebraic neural network theory ...
... or Neuroalgebraic Geometry investigates polynomial neural networks and aims to draw conclusions for arbitrary networks via polynomial approximation. This is done by studying the geometry of the space of functions parametrized by a fixed neural network architecture, known as its neuromanifold (see figure above). For polynomial networks, their neuromanifolds are semialgebraic sets. Training such a network means to solve an optimization problem over its neuromanifold. Thus, a complete understanding of its intricate geometry would shed light on the mysteries of deep learning. The algebraic perspective enables a more concrete understanding of the loss landscape, which is the graph of the loss function over the neuromanifold. The goal of this project is to compare the geometry of neuromanifolds of different architectures to 1) understand the different training behavior experienced by different architectures, 2) find theoretical criteria that predict how well different architectures perform on a concrete given task (such as 3D reconstruction), and 3) design energy-efficient networks. Concrete examples of key geometric features that should be determined for neuromanifolds are their singularities, boundary points, and hidden parameter symmetries, as well as their effect on efficient optimization and good generalization.
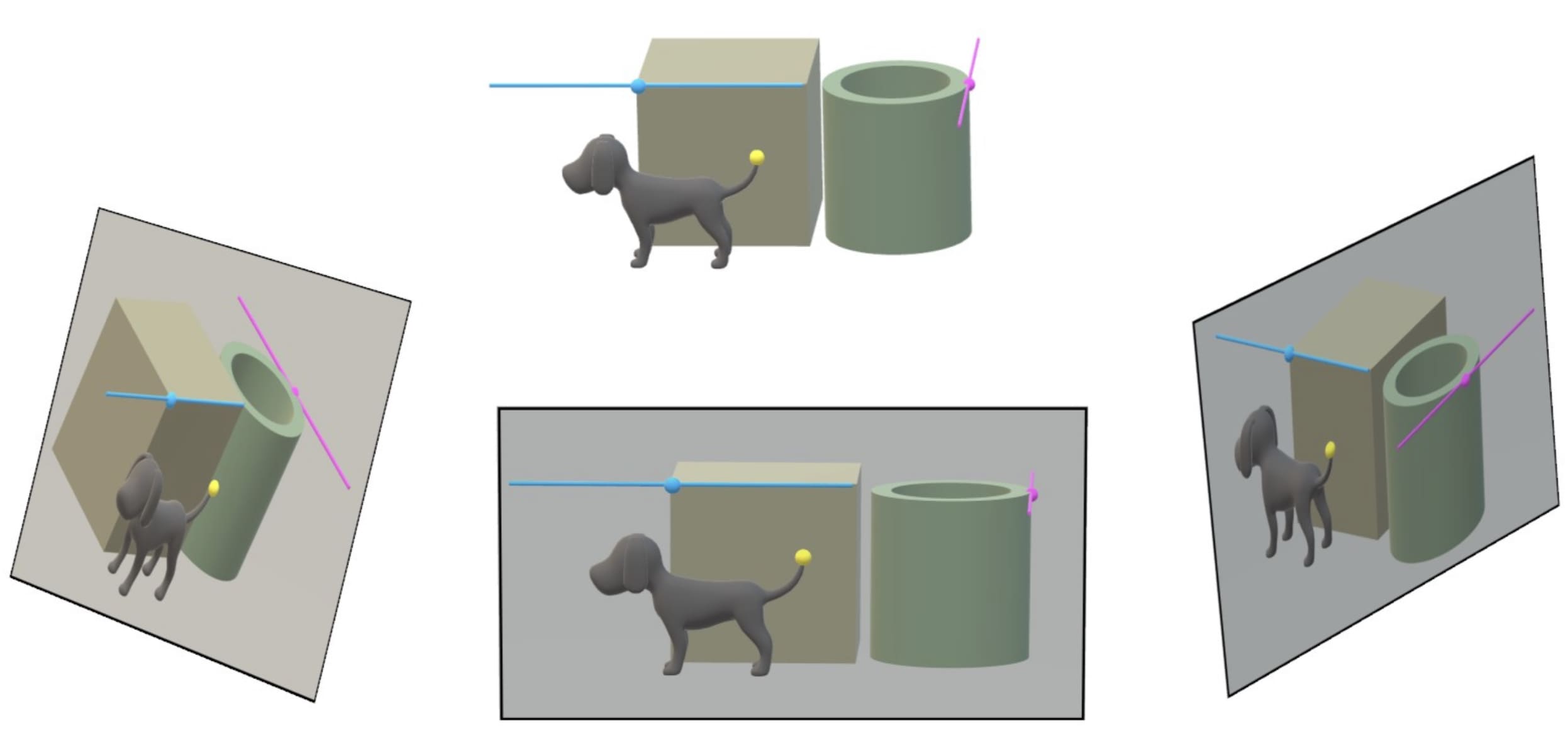
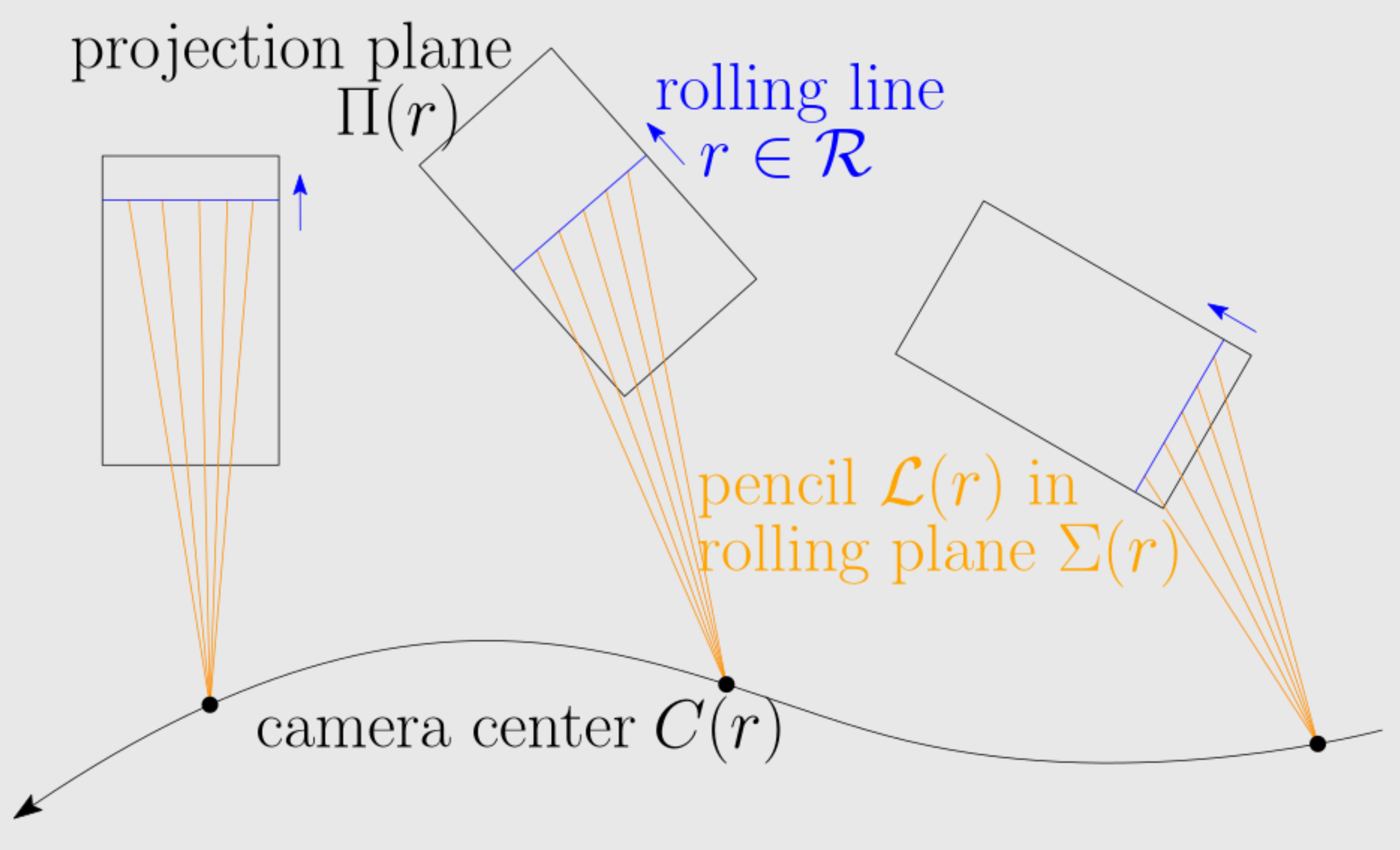
Algebraic vision ...
... is the two-way street between algebraic geometry and computer vision. Implementing fast 3D reconstruction algorithms for rolling-shutter cameras - without restricting assumptions - is a major open challenge in computer vision. Algebraic geometry provides the natural tools for rigorous theoretical foundations for that challenge. Images of rolling-shutter cameras have peculiar features: A 3D point can appear more than once on the same image, and 3D lines become higher-degree image curves. Thus, the existing theory for traditional global-shutter cameras does not apply. From the algebro-geometric perspective, rolling-shutter cameras parametrize algebraic surfaces in the Grassmannian of 3D lines, and 3D reconstruction amounts to computing fibers under rational maps. The project will exploit this inherent geometry to 1) find complete catalogs of efficiently solvable algebraic reconstruction problems (so-called minimal problems), 2) develop new intersection-theoretic tools to measure their intrinsic complexity, and 3) describe the critical loci of 3D reconstruction where problem instances are ill-conditioned and prone to numerical instability. If successful, the algebro-geometric foundations developed in this project will lead to the implementation of fast 3D reconstruction algorithms with rolling-shutter cameras.
